Ch.5 오차역전파법/ 5.6 Affine/Softmax 계층 구현

5.6.1 Affine 계층

 

신경망의 순전파에서 가중치 신호의 총합을 계산하기 위해서 행렬의 내적을 사용하였다. 이를 Computational Graph로 표현한다면

다음 과 같다. 지금까지의 그래프는 노드 사이에 '스칼라값'이 흘렀는데 반해, 이 예에서는 '행렬'이 흐르고 있다.

 

역전파에 대해서 구해보면 

다음과 같은데, 행렬 혹은 벡터에 대한 미분에 대한 증명으로

https://nbviewer.jupyter.org/github/metamath1/ml-simple-works/blob/master/fitting/matrix-derivative.ipynb

Jupyter Notebook Viewer

다음 게시글을 참고하며 정리해보았다. 대충 증명에 대한 것이므로, 읽지 않아도 무관하다.

 

5.6.2 배치용 Affine 계층

 

위 예시에서는 입력 데이터로 X하나만 고려하였다. 그렇다면 데이터 N개를 묶어 순전파 하는 경우는 어떻게 될까?

**3번 방향의 역전파를 보면 행렬 -> 벡터 가 된 것을 볼 수 있다. 이는 값을 합쳐주면 된다.

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
        
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W)+self.b
        
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

 

5.6.3 Softmax-with-Loss 계층

 

소프트맥스 함수는 입력 값을 정규화하여 출력한다.

이 책에서는 손글씨 숫자 인식(Mnist)을 예시로 들고 있다.

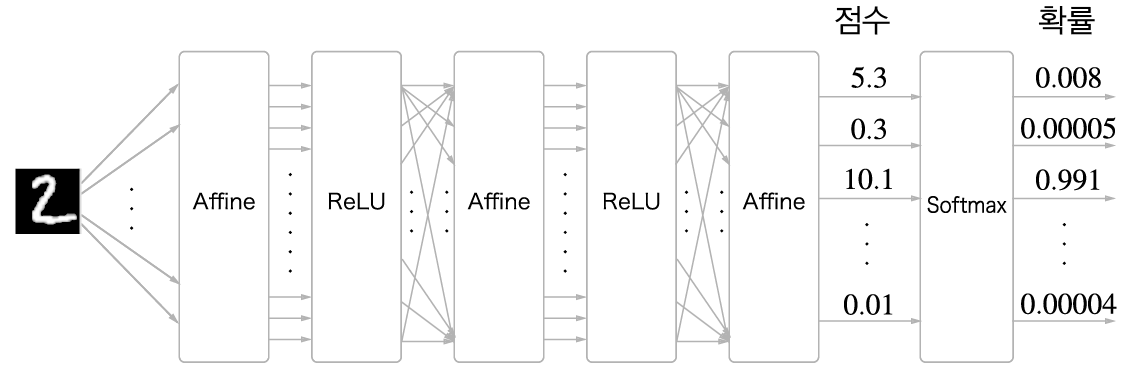
Softmax 계층은 입력 값을 정규화 (출력의 합이 1이 되도록 변형)하여 출력한다. 

 

Softmax-with-Loss는 손실 함수인 교차 엔트로피 오차까지 포함하는 계층이다. Computational Graph와 간소화된 버전 두 개를 살펴보자

Computational Graph of the Softmax-with-Loss layer

간소화된 버전

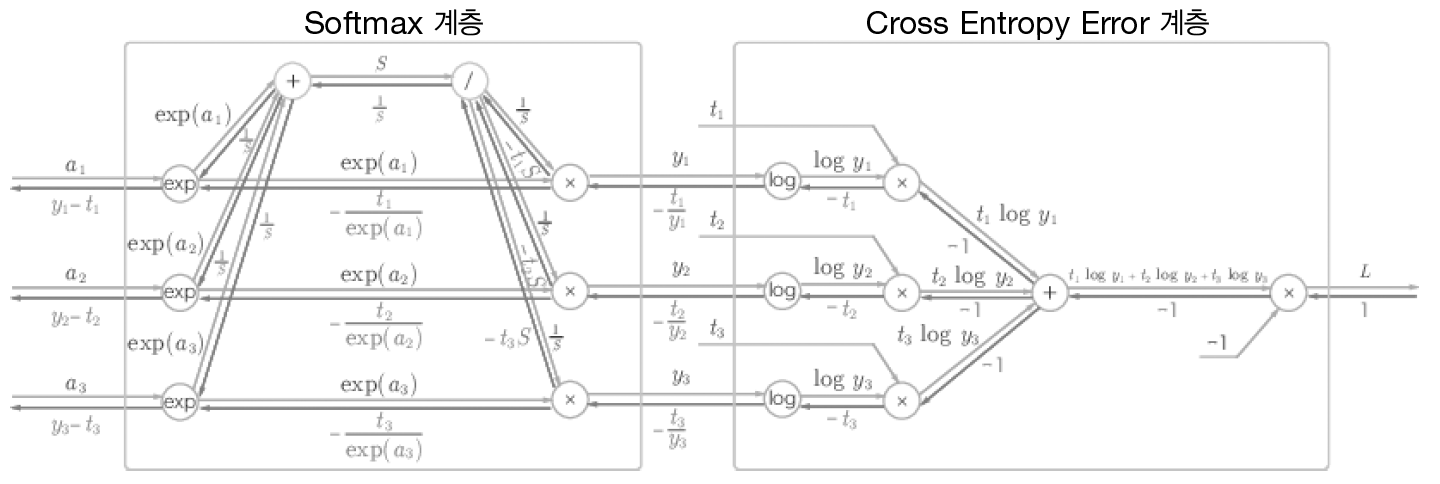
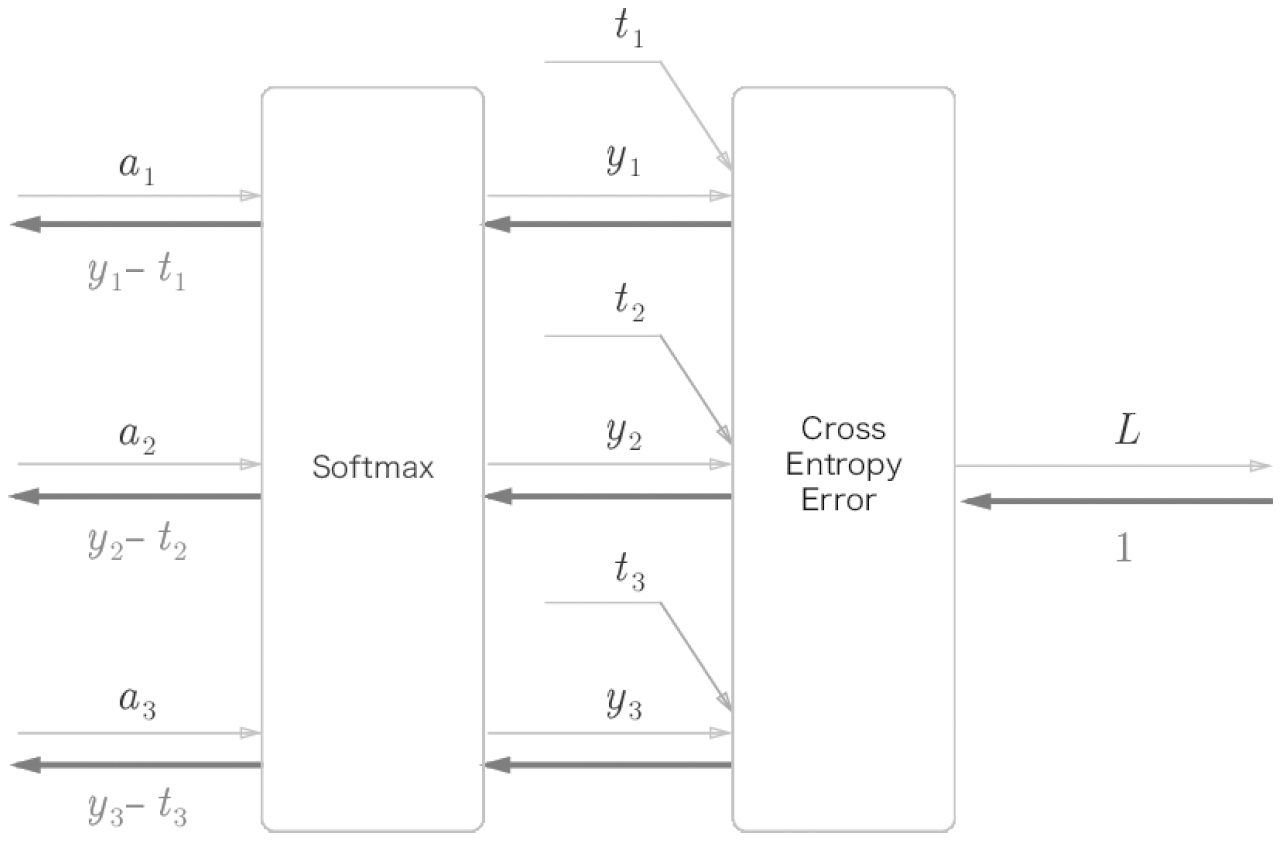
여기에서는 3클래스 분류를 가정하고 이전 계층에서 3개의 입력(점수)를 받는다.

• Softmax 계층은 입력 (a1, a2, a3)를 정규화하여 (y1, y2, y3)를 출력한다.
• Cross Entropy Error 계층은 Softmax의 출력 (y1, y2, y3)와 정답 레이블 (t1, t2, t3)를 받고, 손실 L을 출력한다.

여기서 주목해야 할 것은 역전파의 결과이다. Softmax 계층의 역전파는 (y1 - t1, y2 - t2, y3 - t3)라는 말끔한 결과를 내놓고 있다. 신경망의 역전파에서 이 차이는 오차가 앞 계층에 전해진다는 것이다. 이는 신경망 학습의 중요한 성질이다.

 

신경망 학습의 목적은 신경망의 출력이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이다. 그렇기 때문에 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달하는 것이다. (교차 엔트로피 오차 함수가 다음과 같은 말끔한 결과를 내는 이유는 그렇게 설계되었기 때문이다.)

 

이해가 조금 되지 않는데 예시를 하나 보자

Softmax 계층이 (0.3, 0.2, 0.5)를 출력했으며, 정답 레이블이 (0, 1, 0)이라고 가정하자. 그렇다면 역전파는 (0.3, -0.8, 0.5)이다. 결과적으로 Softmax 계층의 앞 계층들은 이런 오차로부터 큰 깨달음을 얻게 된다. (학습이 많이 필요하다는 뜻)

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None #softmax 출력
        self.t = None #정답 레이블
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx