5.5.1 ReLU 계층
먼저 활성화 함수로 사용되는 ReLU의 수식이다.

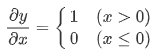
순전파 때의 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘린다, 반면 x가 0보다 작은 경우엔 신호를 보내지 않는다.
Computational Graph로는 다음과 같다.

이제 코드로 옮겨보자
class ReLU:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x<=0)
out =x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx여기서 mask 의 정체에 대해서 알기 어려웠지만 예시를 통한다면 쉽게 파악할 수 있다.
>>>x=np.array([[1.0,-0.5],[-2.0,3.0]])
>>>print(x)
[[ 1. -0.5]
[-2. 3. ]]
>>>mask = (x<=0)
>>>print(mask)
[[False True]
[ True False]]
>>>type(mask)
numpy.ndarray
>>>mask.dtype
dtype('bool')기본적으로 x를 numpy array로 선언하기 때문에 mask 역시 이에 따라서 생성된다. 확인 결과 mask는 bool type의 ndarray임을 알 수가 있다.
>>relu = ReLU()
>>relu.forward(x)
array([[1., 0.],
[0., 3.]])0보다 작은 경우엔 mask가 True가 되어, out의 값을 0으로 만들어버렸다.
>>>out[mask]
array([-0.5, -2. ])
>>>out[mask]=0
>>>out
array([[1., 0.],
[0., 3.]])다음과 같음을 볼 수 있다.
5.5.2 Sigmoid 계층

이를 computational graph로 나타내면 다음과 같다.
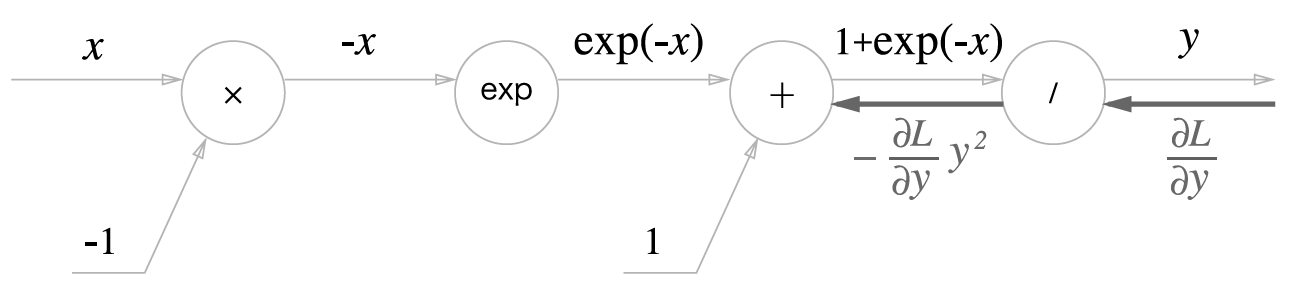
이제 역전파의 흐름대로 한 단계 씩 알아보자.
1단계
'/' 노드를 즉 y = 1/x를 미분하면 다음과 같은 결과를 얻을 수 있다.

해석 하자면, 역전파 때는 순전파의 출력을 제곱한 후 음수값으로 하류로 전달한다.
2단계
'+' 노드는 단순히 값을 하류로 보낸다.
3단계
'exp'노드는 y=exp(x)를 수행하고, 미분과 원함수가 동일하다.

4단계
'x' 노드는 순전파 때의 값을 '서로 바꿔' 곱한다.
이제 전체의 결과를 보자

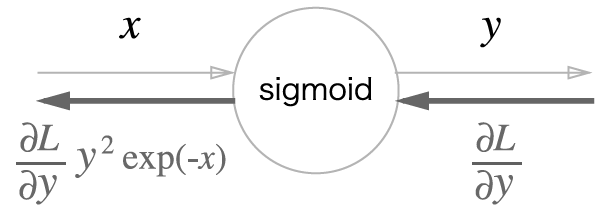
식을 한 번 정리해보자

굉장히 간단해졌다! Sigmoid 계층의 역전파는 순전파의 출력 (y) 만으로 계산할 수 있다.

마지막으로 간단하게 코드로 구현해보자
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1/(1+np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1-self.out)*self.out
return dx이 구현에서는 순전파의 출력을 인스턴스 변수 out에 저장했다가, 역전파 계산 때 그 값을 사용한다.
'머신 러닝 및 파이썬 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| Ch.6 학습 관련 기술들/ 6.2 확률적 경사 하강법 (0) | 2020.03.10 |
|---|---|
| Ch.5 오차역전파법/ 5.6 Affine/Softmax 계층 구현 (0) | 2020.03.05 |
| Ch.5 오차역전파법/ 5.1 계산 그래프, 5.2 연쇄법칙, 5.3 역전파, 5.4 단순한 계층 구현 (0) | 2020.03.03 |
| Ch.4 신경망 학습/ 4.5 학습 알고리즘 구현하기 (0) | 2020.03.03 |
| Python: Lambda 식 (0) | 2020.03.02 |