[벡터와 벡터의 곱셈]
먼저 1차원인 Vector 끼리의 곱셈 먼저 알아보자.
내적 (inner product)에 대해서 알아 볼 것인데, 내적은 사실 여러가지 표현법이 있다.
번역과 표기 덕에 책을 공부하면서 헷갈렸던 부분이다....

<x,y>와 같은 기호로도 표기하고, dot product라고 하기도 한다. 단순히 나열하는 식으로 쓰기 위해서는 행렬의 전치,
Transpose가 필요하다.

NumPy코드 예시를 하나 보자
x = np.array([1,2,3])
y = np.array([3,2,1])
np.dot(x,y)
Out[66]: 10np.dot()이라는 메소드로 계산할 수 있는데, y대신 y.T를 넣어도 된다. 하지만 vector 꼴이기 때문에, Transpose하지 않아도 계산된다.
그렇다면 NumPy의 matrix 꼴에서는 어떤 결과가 나올까?
x=np.array([[1,2,3]])
y=np.array([[3,2,1]])
x.shape
Out[74]: (1, 3)
y.shape
Out[75]: (1, 3)다음과 같이 1X3 행렬을 두 개 만들었다.
np.dot(x,y)
Traceback (most recent call last):
File "<ipython-input-76-6849a5f7ad6c>", line 1, in <module>
np.dot(x,y)
ValueError: shapes (1,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)두 개를 dot product 한 결과 불가능하다고 나온다.
np.dot(x,y.T)
Out[77]: array([[10]])앞서 서술한대로 Transpose한 경우에는 성립한다.
[행렬의 내적과 곱셈]
가볍게 Vector의 곱셈에 대해서 파악해보았으니 Matrix 단에서 알아보자

행렬곱은 기본적으로 모양이 맞아야 가능하다.
간단하게 말해서 위 예시 처럼 두 행렬을 곱하고 싶다면 A(m x k) B(k x n) 처럼 앞 부분의 col과 뒷 부분의 row가 같아야한다.
(m x k) · (k x n) = (m x n)
이 경우에만 행렬곱이 이루어질 수 있다. 한 가지 예시를 보자

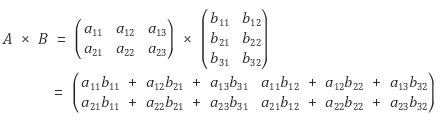
마지막으로 코드를 통한 예시를 하나 보자
np.dot(x,y.T)
Out[77]: array([[10]])
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[1,2],[3,4],[5,6]])
A.shape
Out[80]: (2, 3)
B.shape
Out[81]: (3, 2)
np.dot(A,B)
Out[82]:
array([[22, 28],
[49, 64]])
np.dot(A,B).shape
Out[83]: (2, 2)
다음 두 글을 참고하여 작성하였다.
행렬의 곱셈, 행렬의 거듭제곱
행렬의 곱셈은 행렬의 실수배에 비하면 훨씬 어려워요. 행렬을 곱할 수 있는 조건이 있어 이 조건을 만족하지 않으면 곱셈을 하지 못하는 경우도 있어요. 게다가 계산방식도 매우 까다롭죠. 도형 문제처럼 행렬을..
mathbang.net
https://datascienceschool.net/view-notebook/3f44cfdda2874080a9aa6b034c71d5ec/
'머신 러닝 및 파이썬 > Numpy 공부' 카테고리의 다른 글
| Dictionary 변수 데이터 옮기기 (0) | 2020.03.10 |
|---|---|
| Numpy의 Shape (0) | 2020.03.04 |
| Numpy의 log (0) | 2020.02.27 |
| Numpy의 Dimension (0) | 2020.02.27 |