하노이의 타워는 재귀함수의 효율을 잘 보여주는 예시 중 하나이다.
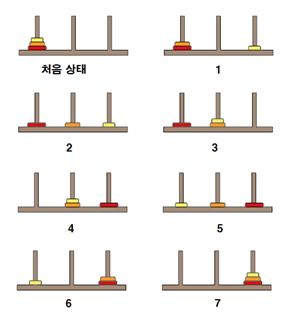
하노이의 타워는 다음과 같은 규칙을 지켜야한다.
- 한 번에 하나의 원판만 옮길 수 있다.
- 큰 원판이 작은 원판 위에 있어서는 안 된다.
크기 순으로 1, 2, 3 이라고 원판을 불러보자.
원판 3이 마지막 막대에 들어가기 위해서는 원판 1,2 가 탑을 이루는 과정이 필요하다.

만약 원판이 하나 더 있다고 가정해보자. 위 파란 글씨의 방식을 생각해본다면
원판 4는 원판 1,2,3이 탑을 이루고 있다면 마지막 막대로 이동할 수 있다.
그 이후는 다음과 같은 과정을 이룰 것이다.
1. 원판 4는 막대 C (막대를 순서대로 A, B, C라고 명명)에 올라간다.
2. 원판 1,2,3은 막대 B에 위치한 상태
3. 원판 4는 제일 크기 때문에 처음부터 없는 상태라고 가정 가능
4. 원판 1,2,3만 존재하는 하노이의 타워의 방법을 취할 수 있음
즉 원판의 갯수가 몇개라고 할 지라도 이러한 연속적인 과정을 통해서 이동 시킬 수 있다.
이러한 연속적인 과정은 재귀함수에서 굉장히 유리하다.
#include <iostream>
using namespace std;
void HanoiTowerMove(int num, char a, char b, char c) {
//num개의 원반을 b를 거쳐 a에서 c로 이동한다.
if (num == 1)
printf("원판1을 %c에서 %c로 이동\n", a, c);
else {
HanoiTowerMove(num - 1, a, c, b); //부분1
printf("원판%d를 %c에서 %c로 이동\n", num, a, c); //부분2
HanoiTowerMove(num - 1, b, a, c); //부분3
}
}
int main() {
int input;
cout << "원판의 갯수 입력:";
cin >> input;
HanoiTowerMove(input, 'A', 'B', 'C');
system("pause");
return 0;
}HanoiTowerMove 함수는 세 부분으로 나눌 수 있다.
1. 맨 아래의 원판을 제외하고 A에서 B로 이동시키기
2. 맨 아래의 원판을 A에서 C로 이동시키기
3. B로 이동한 원판들을 모두 C로 이동시키기
이런 과정을 통해서 재귀적으로 모든 원판을 이동시킬 수 있다.
마지막으로 백준에서 하노이의 탑 문제를 소개하고 마친다.
https://www.acmicpc.net/problem/1914
1914번: 하노이 탑
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다. 이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다. 아래 그림은 원판이 5
www.acmicpc.net
ps... 만들고 보니 하노이의 탑보다는 biginteger문제가 더 문제인 문제였다..
'자료구조' 카테고리의 다른 글
| 힙 (Heap) (0) | 2020.01.29 |
|---|---|
| 링크드 리스트 (Linked List) (0) | 2020.01.26 |
| 배열리스트 (ArrayList) (0) | 2020.01.26 |